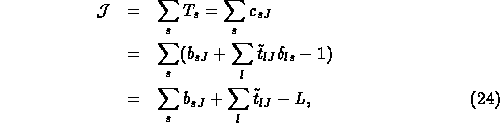DUALITY-BASED A POSTERIORI ERROR ESTIMATES FOR SOME APPROXIMATION SCHEMES FOR CONVEX OPTIMAL CONTROL PROBLEMS
A note on the duality gap in nonconvex optimization and a very simple procedure for bid evaluation type prob|ems
Mind the duality gap: safer rules for the Lasso | DeepAI
On the Duality Gap in Nonconvex Optimization
A Comparative Study of Three Different Mathematical Methods for Solving the Unit Commitment Problem
Convex Optimization - Duality Gap
![PDF] A Duality Theory with Zero Duality Gap for Nonlinear Programming | Semantic Scholar](https://d3i71xaburhd42.cloudfront.net/6810c435620f7cffe800fea3e77c198d79e7dc64/7-Figure1-1.png "PDF] A Duality Theory with Zero Duality Gap for Nonlinear Programming | Semantic Scholar")
PDF] A Duality Theory with Zero Duality Gap for Nonlinear Programming | Semantic Scholar
Conditions for zero duality gap in convex programming - CARMA ...
![PDF] DUALITY GAP ESTIMATION VIA A REFINED | Semantic Scholar](https://d3i71xaburhd42.cloudfront.net/e0c09c654e2e5316fb581a5a6ca48a3cdd1fec1b/16-Figure2-1.png "PDF] DUALITY GAP ESTIMATION VIA A REFINED | Semantic Scholar")
PDF] DUALITY GAP ESTIMATION VIA A REFINED | Semantic Scholar
arXiv:1811.05512v2 [cs.LG] 15 Jul 2020
Duality and KKT Conditions
Publications and Press
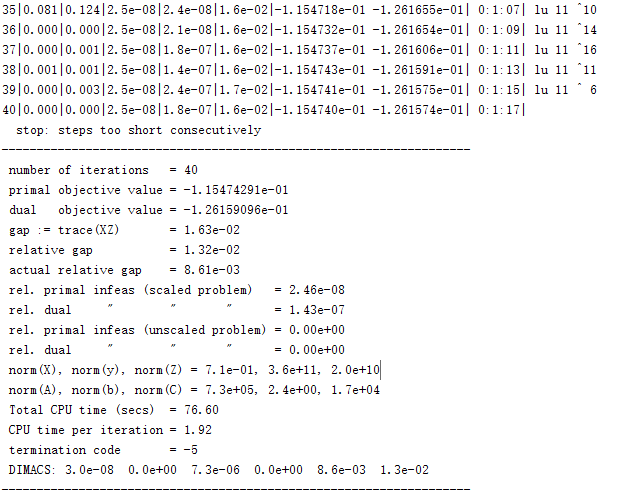
Is it possible to reduce the large duality gap by changing solver settings? - CVX Forum: a community-driven support forum
Paper read with more formula derivation: Semidefinite Programmin | 码农家园
arXiv:1012.5568v1 [math.OC] 27 Dec 2010
Untitled
Lec11 rate distortion optimization
Distributed Primal-Dual Optimization for Non-uniformly Distributed Data
Duality-Gap Bounds for Multi-Carrier Systems and Their Application to Periodic Scheduling
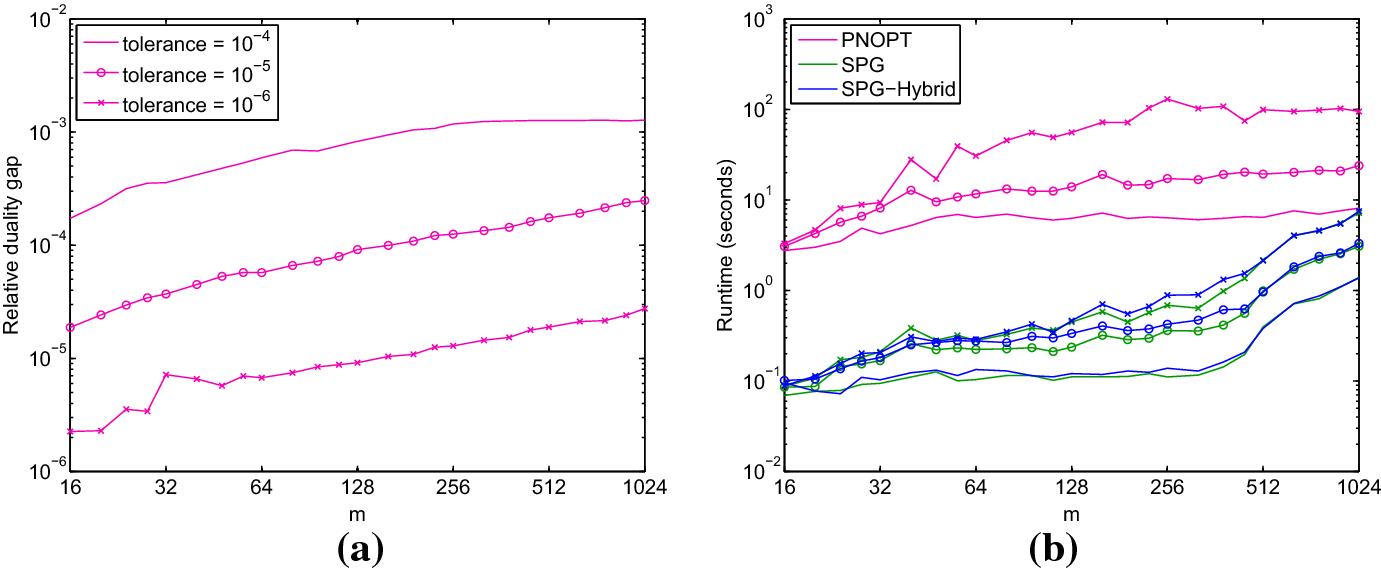
Figure 4 | A hybrid quasi-Newton projected-gradient method with application to Lasso and basis-pursuit denoising | SpringerLink
Characterizations of ɛ-duality gap statements for constrained optimization problems – topic of research paper in Mathematics. Download scholarly article PDF and read for free on CyberLeninka open science hub.
What is the intuitive explanation for the duality in optimization? Why are the primal problem and the dual problem equivalent? - Quora
Lecture 1
Inherent Duality Gap
PPT - Exploiting Duality (Particularly the dual of SVM) PowerPoint Presentation - ID:1017623
Duality Theorems - Nonlinear Programming - Lecture Slides - Docsity
Zero Duality Gap in Optimal Power Flow Problem
Chapter 3: Convexity Chapter 4: Primal optimality conditions Chapter 5: Primal–dual optimality conditions Chapter 6: Lagrangia
